How Do You Know How Many Ovals You Should Use? How Do You Know What to Put Inside the Ovals?
Y'all've probably learned a lot about shapes without ever actually thinking about what they are. Merely understanding what a shape is is incredibly handy when comparison information technology to other geometric figures, such as planes, points, and lines. In this article, we'll cover what exactly a shape is, likewise as a agglomeration of common shapes, what they look like, and the major formulas associated with them. If someone asks you what a shape is, you lot'll likely be able to name quite a few of them. But "shape" has a specific significant, too—it'south non just a name for circles, squares, and triangles. A shape is the form of an object—not how much room information technology takes upward or where it is physically, but the bodily form information technology takes. A circle isn't divers by how much room it takes up or where you see it, but rather the actual round class that it takes. A shape can be any size and appear anywhere; they're not constrained past annihilation because they don't actually take up whatever room. It's kind of hard to wrap your listen around, but don't call up of them as being physical objects—a shape tin can exist 3-dimensional and take upwardly physical room, such as a pyramid-shaped bookend or a cylinder can of oatmeal, or it can exist 2-dimensional and take up no physical room, such as a triangle drawn on a slice of paper. The fact that it has a form is what differentiates a shape from a bespeak or a line. A point is just a position; it has no size, no width, no length, no dimension whatsoever. A line, on the other paw, is one-dimensional. It extends infinitely in either direction and has no thickness. It'south non a shape because information technology has no form. Though we may represent points or lines equally shapes considering we need to really see them, they don't really have any class. That's what differentiates a shape from the other geometric figures—information technology'due south 2- or three-dimensional, because it has a class. Picturing a shape only based on definition is difficult—what does information technology mean to have form but not accept up space? Permit's accept a look at some dissimilar shapes to better sympathize what exactly it means to be a shape! We frequently classify shapes by how many sides they accept. A "side" is a line segment (part of a line) that makes up part of a shape. Just a shape can take an cryptic number of sides, too. Ellipses are round, oval shapes in which a given point (p) has the aforementioned sum of distance from ii different foci. An oval looks a bit like a smooshed circle—rather than being perfectly round, it'south elongated in some way. Even so, the classification is imprecise. At that place are many, many kinds of ovals, but the general significant is that they are a round shape that is elongated rather than perfectly round, as a circle is.An oval is any ellipses where the the foci are in two different positions. Considering an oval is not perfectly round, the formulas we apply to empathize them take to be adjusted. It's too important to notation that calculating the circumference of an oval is quite difficult, so there'south no circumference equation below. Instead, employ an online calculator or a calculator with a built-in circumference function, because even the all-time circumference equations you can practice by hand are approximations. Definitions How many sides does a circle accept? Expert question! There's no good respond, unfortunately, because "sides" take more to practice with polygons—a two-dimensional shape with at least 3 straight sides and typically at least 5 angles. Almost familiar shapes are polygons, but circles have no straight sides and definitely lack five angles, then they are not polygons. So how many sides does a circle have? Zero? 1? It'south irrelevant, actually—the question simply doesn't employ to circles. A circle isn't a polygon, but what is it? A circle is a two-dimensional shape (it has no thickness and no depth) fabricated upwards of a curve that is e'er the aforementioned distance from a point in the centre.An oval has ii foci at different positions, whereas a circle's foci are e'er in the same position. Definitions Formulas Triangles are the simplest polygons. They accept three sides and three angles, but they can look different from 1 another. Yous might have heard of right triangles or isosceles triangles—those are unlike types of triangles, simply all volition have iii sides and 3 angles. Definitions Formulas A parallelogram is a shape with equal opposite angles, parallel opposite sides, and parallel sides of equal length. You might notice that this definition applies to squares and rectangles—that's considering squares and rectangles are also parallelograms! If you tin can calculate the surface area of a square, you can do information technology with any parallelogram. Definitions Formulas A rectangle is a shape with parallel opposite sides, combined with all 90 degree angles. As a blazon of parallelogram, it has opposite parallel sides. In a rectangle, ane ready of parallel sides is longer than the other, making information technology look like an elongated square. A foursquare is a lot similar a rectangle, with one notable exception: all its sides are equal length. Like rectangles, squares have all 90 degree angles and parallel reverse sides. That'south because a square is actually a type of rectangle, which is a type of parallelogram! For that reason, you can use the same formulas to calculate the area or perimeter of a square as y'all would for whatsoever other parallelogram. A rhombus is—you lot guessed it—a type of parallelogram. The deviation between a rhombus and a rectangle or square is that its interior angles are only the same equally their diagonal opposites. Because of this, a rhomb looks a bit like a square or rectangle skewed a bit to the side. Though perimeter is calculated the aforementioned way, this affects the way that y'all calculate the surface area, because the top is no longer the same as it would be in a square or rectangle. Definition Formulas Trapezoids are 4-sided figures with two reverse parallel sides. Different a parallelogram, a trapezoid has just two opposite parallel sides rather than 4, which impacts the manner y'all calculate the area and perimeter. Definitions Formulas A pentagon is a five-sided shape. We typically see regular pentagons, where all sides and angles are equal, simply irregular pentagons likewise exist. An irregular pentagon has unequal side and unequal angles, and tin can be convex—with no angles pointing inward—or concave—with an internal angle greater than 180 degrees. Because the shape is more complex, it needs to exist divided into smaller shapes to summate its expanse. Definitions Formulas A hexagon is a six-sided shape that is very similar to pentagon. We most frequently see regular hexagons, merely they, like pentagons, tin also be irregular and convex or concave. Also like pentagons, a hexagon'southward area formula is significantly more complex than that of a parallelogram. Formulas There are also three-dimensional shapes, which don't just have a length and a width, but too depth or book. These are shapes you come across in the existent world, similar a spherical basketball, a cylindrical container of oatmeal, or a rectangular book. Three-dimensional shapes are naturally more circuitous than two-dimensional shapes, with an boosted dimension—the amount of space they take up, not just the form—to include when calculating surface area and perimeter. Math involving 2d shapes, such as those above, is called plane geometry because it deals specifically with planes, or flat shapes. Math involving 3D shapes like spheres and cubes is called solid geometry, because it deals with solids, some other give-and-take for 3D shapes. 2d shapes make upward the 3D shapes we see every twenty-four hour period! At that place are and so many types of shapes that it can be tricky to recollect which is which and how to summate their areas and perimeters. Here'southward a few tips and tricks to help you recollect them! Some shapes are polygons and some are not. Ane of the easiest ways to narrow downwards what type of shape something is is figuring out if it'due south a polygon. A polygon is comprised of direct lines that exercise non cross. Which of the shapes below are polygons and which are not? The circumvolve and oval are not polygons, which means their surface area and perimeter are calculated differently. Learn more most how to calculate them using $π$ to a higher place! If the shape you're looking at is a parallelogram, it'due south generally easier to calculate its area and perimeter than if it isn't a parallelogram. Merely how do yous identify a parallelogram? It's correct at that place in the name—parallel. A parallelogram is a 4-sided polygon with two sets of parallel sides. Squares, rectangles, and rhombuses are all parallelograms. Squares and rectangles use the same basic formulas for surface area—length times height. They're also very piece of cake to find perimeter for, as you just add all the sides together. Rhombuses are where things get catchy, because you lot multiply the diagonals together and divide past 2. To determine what kind of parallelogram you're looking at, ask yourself if it has all 90-degree angles. If yep, it's either a foursquare or a rectangle. A rectangle has two sides that are slightly longer than the others, whereas a square has sides of all equal length. Either mode, y'all calculate the surface area by multiplying the length times the tiptop and perimeter past adding all four sides together. If no, it'due south probably a rhomb, which looks like if yous took a foursquare or rectangle and skewed information technology in either direction. In this case, you'll find the area by multiplying the 2 diagonals together and dividing by two. Perimeter is plant the aforementioned way that yous would find the perimeter of a square or rectangle. Formulas for shapes that don't have four sides can become quite tricky, so your best bet is to memorize them. If you have trouble keeping them directly, try memorizing the Greek words for numbers, such as: Tri: three, as in triple, significant three of something Tetra: four, as in the number of squares in a Tetris block Penta: five, every bit in the Pentagon in Washington D.C., which is a large building in the shape of a Pentagon Hexa: six, as in hexadecimal, the six-digit codes often used for color in web and graphic design Septa: seven, as in Septa, the female clergy of Game of Thrones' religion, which has seven gods Octo: eight, every bit in the eight legs of an octopus Ennea: 9, as in an enneagram, a mutual model for human personalities Deca: x, as in a decathlon, in which athletes complete ten events If you're prepping for the Human activity and want a little additional help on your geometry, check out this guide to coordinate geometry! If you're more the SAT blazon, this guide to triangles on the Sabbatum geometry section will assistance you prepare for the test! Can't go enough of Human action math? This guide to polygons on the Deed will help you prepare with useful strategies and practice issues! 
What Is a Shape?
 Cubes, like those seen here, are three-dimensional forms of squares—both are shapes!
Cubes, like those seen here, are three-dimensional forms of squares—both are shapes! The 6 Main Types of Ii-Dimensional Geometric Shapes
Type 1: Ellipses
Oval
Formulas
Circle

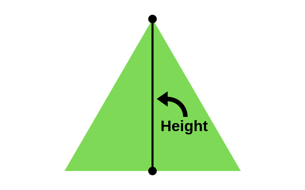
Blazon 2: Triangles

Because there are many kinds of triangles, there are lots of important triangle formulas, many of them more complex than others. The basics are included below, simply even the basics rely on knowing the length of the triangle's sides. If you don't know the triangle'southward sides, you can still calculate different aspects of it using angles or only some of the sides.
Type 3: Parallelograms

Rectangle

Because a rectangle is a parallelogram, you can utilize the exact same formulas to calculate their expanse and perimeters.Square

Rhombus
Type iv: Trapezoids

Type 5: Pentagons

Type 6: Hexagons

What About 3-Dimensional Geometric Shapes?

3 Key Tips for Working With Shapes
#one: Identify Polygons

#two: Cheque for Parallel Sides
#3: Count the Number of Sides
What'due south Next?

About the Author
Melissa Brinks graduated from the University of Washington in 2014 with a Bachelor's in English with a creative writing emphasis. She has spent several years tutoring K-12 students in many subjects, including in SAT prep, to aid them prepare for their higher instruction.
Source: https://blog.prepscholar.com/geometric-shapes-names-list
0 Response to "How Do You Know How Many Ovals You Should Use? How Do You Know What to Put Inside the Ovals?"
Post a Comment